Esta web utiliza cookies para que podamos ofrecerte la mejor experiencia de usuario posible. La información de las cookies se almacena en tu navegador y realiza funciones tales como reconocerte cuando vuelves a nuestra web o ayudar a nuestro equipo a comprender qué secciones de la web encuentras más interesantes y útiles.
Nuestro Blog
Las variables nominales son algo más que un nombre
El análisis de variables nominales es algo muy común en los ensayos clínicos. Si quieres saber más sobre cómo analizar este tipo de variables, ¡sigue leyendo!
Por Mercedes Ovejero y Jaime Ballesteros
Unidad de Bioestadística de Sermes CRO
El análisis de variables nominales es algo muy común en los ensayos clínicos. Si quieres saber más sobre cómo analizar este tipo de variables, ¡sigue leyendo!
Por Mercedes Ovejero y Jaime Ballesteros
Unidad de Bioestadística de Sermes CRO
¿Qué son las variables nominales?
Las variables nominales son un tipo de variables categóricas que toman diversos valores en los que el orden no importa. Son variables que ayudan a diferenciar unos elementos de otros por sus cualidades y no por su cantidad o su grado de posesión de determinada modalidad.
Ejemplos de variables nominales clásicas en los ensayos clínicos son el grupo de aleatorización, el sexo, el diagnóstico, el tipo de tratamiento, el hospital donde se han reclutado los pacientes, si se ha realizado o no determinada prueba médica, el tipo de acontecimiento adverso, etc. Otras variables nominales pueden ser cualquiera que sea identificativa, por ejemplo: el nombre completo de la persona, el número de DNI, el número de pedido, el número de teléfono, el número de historia clínica, etc.
Primero describir…
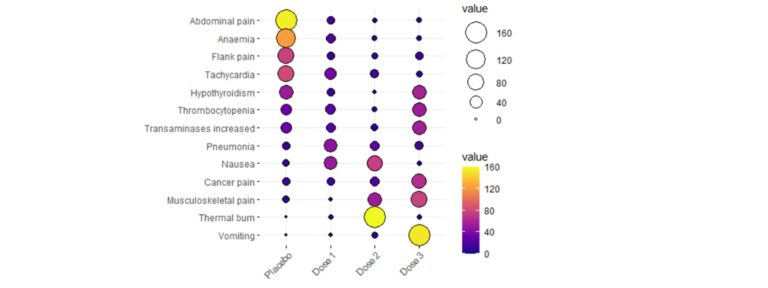
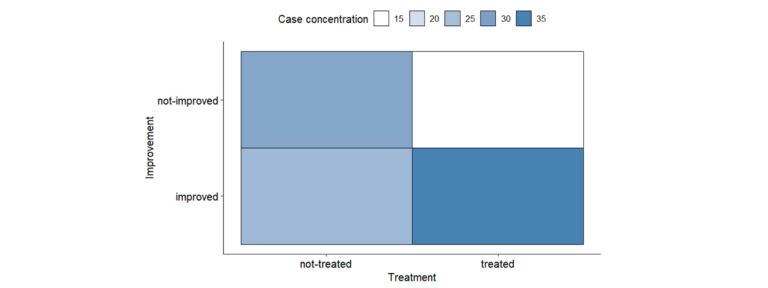
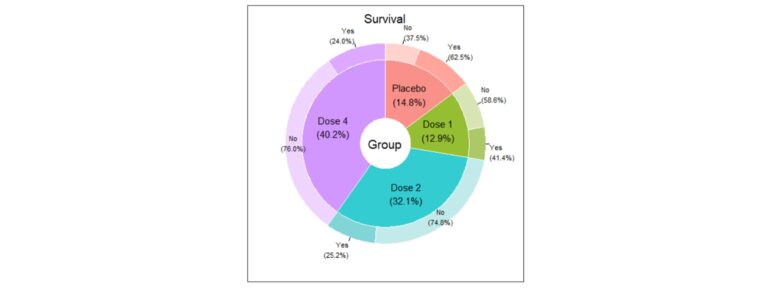
El análisis descriptivo de las variables nominales suele comenzar con el estudio de su distribución del número de casos en cada categoría y los porcentajes. Además, es esencial representarlas gráficamente de forma clara. Gráficas clásicas son el diagrama de barras o el de sectores, pero, en el caso de querer representar varias variables de forma simultánea y muy visual, se exponen a continuación algunos ejemplos:
Asociación entre variables nominales, ¿por qué no ser amig@s?
El análisis para estudiar la relación entre dos variables nominales parte, en numerosas ocasiones, del estudio del coeficiente ji-cuadrado. Es uno de los análisis más conocidos y ampliamente utilizados en cualquier área de la Ciencia. Este análisis tiene una serie de supuestos, pero uno de los más importantes está asociado a las frecuencias esperadas conjuntas, según el cual no más del 20% de las casillas debe tener una frecuencia esperada inferior a 5 casos. Cuando este supuesto no se cumple, la prueba pierde potencia. Cuando se analizan correlaciones con este coeficiente, hay que tener en cuenta una serie de matices:
- Si la tabla es de 2×2, se debe de utilizar la corrección por continuidad de Yates.
- Si el tamaño muestral es muy pequeño, inferior a 30 casos y se dispone de una tabla 2×2, se debe de utilizar la prueba exacta de Fisher.
Dado que el coeficiente ji-cuadrado no está acotado (su valor oscila entre 0 e infinito), no es posible estudiar la intensidad de la correlación, aunque los análisis de residuos permiten estudiar la concentración de casos en las casillas de la tabla de contingencias.
Existen otros coeficientes que permiten aproximarse al estudio de la intensidad de la asociación entre dos variables nominales:
Nombre | Uso | Rango de valores | Interpretación | Precauciones |
Coeficiente Phi | Tablas de dimensiones 2×2 | Entre -1 y 1 | Si se aproxima a -1 los datos se agrupan en la diagonal principal de la tabla de contingencias. Si se aproxima a 1 los datos se agrupan en la diagonal secundaria de la tabla de contingencias | – |
Coeficiente de contingencia | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | Su valor máximo depende del tamaño de la tabla y su máximo puede estimarse gracias al Cmax. Para comparar tablas de diferentes dimensiones se puede usar la corrección de Pawlik, el cual oscila entre 0 y 1. |
Coeficiente V de Cramer | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | – |
Coeficiente T de Tschuprow | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | – |
Lambda de Goodman-Kruskal | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Coeficiente Q de Yules | 2×2 | Entre -1 y 1 | Según se acerca a 1, la odds ratio será superior a 1. Según se acerca -1 la odds ratio será menor que 1. | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Coeficiente de incertidumbre (U de Thiel) | 2×2 | Entre 0 y 1 | Refleja la reducción proporcional en el error cuando se utilizan los valores de una variable para pronosticar los valores de la otra variable | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Si las variables nominales cambian con el paso del tiempo… ¡síguelas de cerca!
Si se dispone de una variable nominal que se mide en varios periodos temporales y se quiere estudiar si hay cambios en la distribución de sus modalidades, existen una serie de técnicas que permiten estudiar si hay variaciones significativas:
Nombre | Uso | Precauciones | Interpretación |
Prueba de McNemar | Una variable con dos modalidades (evaluación en dos momentos temporales diferentes) | Estas pruebas tienen una serie de supuestos que se deben de vigilar para no perder potencia estadística | Si la prueba es significativa, existirán cambios asociados al paso del tiempo en la distribución de frecuencias de la variable analizada
|
Prueba de Bowker | Una variable con tres o más modalidades (evaluación en dos momentos temporales diferentes) | ||
Prueba Q de Cochran | Una variable con dos modalidades (evaluación en tres o más momentos temporales diferentes) | En el caso de que la prueba sea significativa, se deben de hacer comparaciones múltiples ajustando el nivel de significación |
Unas palabras sobre las odds ratio y el Índice de Riesgo Relativo
Para poder entender el concepto de odds ratio hay que entender los siguientes conceptos asociados a ella:
- Probabilidad: La probabilidad es una medida que señala que tan posible es que ocurra un fenómeno o evento. Este valor oscila entre 0 y 1, siendo 0 que el evento no puede suceder y 1 que el evento ocurre seguro. Por ejemplo, si la probabilidad de mejorar es 0.60, la de no mejorar sería 0.40.
- Odds: es la probabilidad de que suceda un evento dividido por la probabilidad de que no suceda.
Las odds oscilan entre 0 e infinito y se pueden calcular para la ocurrencia del evento como para la no ocurrencia del evento. En el ejemplo, existirían dos odds: la odds de mejorar sería 0.60/0.40=1.5 y la de no mejorar sería 0.40/0.60=0.667. Se interpretan como ratios, es decir, la cantidad de veces que algo pueda suceder sobre que no pueda suceder. En este caso, es más probable que el paciente mejore.
Las odds ratio (OR) supone el cociente entre las dos odds y también oscilan entre 0 e infinito, pero ¿cómo se interpreta una OR de forma básica?
- Cuando la OR es 1 indica ausencia de asociación entre las variables.
- Los valores menores de 1 señalan una asociación negativa entre las variables y los valores mayores de 1 indican asociación positiva entre las variables.
- Cuanto más se aleje la OR de 1, más intensa es la relación.
En el caso del Índice de Riesgo Relativo, se define como el cociente de las probabilidades de tener la enfermedad o presentar el resultado de interés si está presente o ausente el factor predictivo, el factor de riesgo.
Para interpretar el riesgo relativo, pensemos en un RR de 2. Este resultado expresa que el riesgo en un grupo es el doble que en el otro grupo. Si es igual a 1, es igual para ambos grupos y si es menor que 1, el riesgo es mayor para el otro grupo.
La principal diferencia con la OR es que el Índice de Riesgo Relativo se usa fundamentalmente en la evaluación de trabajos prospectivos mientras que el OR se usa principalmente en el análisis de trabajos retrospectivos.
¿Se puede hacer algo más con las variables nominales?
¡Por supuesto que sí! El análisis de las variables nominales puede ir más allá de estudiar su comportamiento descriptivo y su relación bivariada. Algunos ejemplos de análisis que se pueden hacer:
- Modelos loglineales: si se quiere analizar la relación entre tres o más variables nominales.
- Algoritmos de machine learning de clasificación: si se quiere, por ejemplo, pronosticar la probabilidad de que un paciente se recupere (o no) en función de una serie de variables clínicas, estos algoritmos son de gran utilidad.
Análisis de textos y respuestas abiertas: los análisis vinculados al Procesamiento del Lenguaje Natural están al servicio del análisis de textos, por ejemplo, de respuestas abiertas dadas durante una entrevista a los pacientes para conocer su estado de salud.
Asociación entre variables nominales, ¿por qué no ser amig@s?
El análisis para estudiar la relación entre dos variables nominales parte, en numerosas ocasiones, del estudio del coeficiente ji-cuadrado. Es uno de los análisis más conocidos y ampliamente utilizados en cualquier área de la Ciencia. Este análisis tiene una serie de supuestos, pero uno de los más importantes está asociado a las frecuencias esperadas conjuntas, según el cual no más del 20% de las casillas debe tener una frecuencia esperada inferior a 5 casos. Cuando este supuesto no se cumple, la prueba pierde potencia. Cuando se analizan correlaciones con este coeficiente, hay que tener en cuenta una serie de matices:
- Si la tabla es de 2×2, se debe de utilizar la corrección por continuidad de Yates.
- Si el tamaño muestral es muy pequeño, inferior a 30 casos y se dispone de una tabla 2×2, se debe de utilizar la prueba exacta de Fisher.
Dado que el coeficiente ji-cuadrado no está acotado (su valor oscila entre 0 e infinito), no es posible estudiar la intensidad de la correlación, aunque los análisis de residuos permiten estudiar la concentración de casos en las casillas de la tabla de contingencias.
Existen otros coeficientes que permiten aproximarse al estudio de la intensidad de la asociación entre dos variables nominales:
Nombre | Uso | Rango de valores | Interpretación | Precauciones |
Coeficiente Phi | Tablas de dimensiones 2×2 | Entre -1 y 1 | Si se aproxima a -1 los datos se agrupan en la diagonal principal de la tabla de contingencias. Si se aproxima a 1 los datos se agrupan en la diagonal secundaria de la tabla de contingencias | – |
Coeficiente de contingencia | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | Su valor máximo depende del tamaño de la tabla y su máximo puede estimarse gracias al Cmax. Para comparar tablas de diferentes dimensiones se puede usar la corrección de Pawlik, el cual oscila entre 0 y 1. |
Coeficiente V de Cramer | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | – |
Coeficiente T de Tschuprow | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | – |
Lambda de Goodman-Kruskal | Tablas de cualquier tamaño | Entre 0 y 1 | Según se aproxima a 1, la relación es más intensa | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Coeficiente Q de Yules | 2×2 | Entre -1 y 1 | Según se acerca a 1, la odds ratio será superior a 1. Según se acerca -1 la odds ratio será menor que 1. | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Coeficiente de incertidumbre (U de Thiel) | 2×2 | Entre 0 y 1 | Refleja la reducción proporcional en el error cuando se utilizan los valores de una variable para pronosticar los valores de la otra variable | Requiere conocer cuál es la variable independiente y cuál es la dependiente |
Si las variables nominales cambian con el paso del tiempo… ¡síguelas de cerca!
Si se dispone de una variable nominal que se mide en varios periodos temporales y se quiere estudiar si hay cambios en la distribución de sus modalidades, existen una serie de técnicas que permiten estudiar si hay variaciones significativas:
Nombre | Uso | Precauciones | Interpretación |
Prueba de McNemar | Una variable con dos modalidades (evaluación en dos momentos temporales diferentes) | Estas pruebas tienen una serie de supuestos que se deben de vigilar para no perder potencia estadística | Si la prueba es significativa, existirán cambios asociados al paso del tiempo en la distribución de frecuencias de la variable analizada
|
Prueba de Bowker | Una variable con tres o más modalidades (evaluación en dos momentos temporales diferentes) | ||
Prueba Q de Cochran | Una variable con dos modalidades (evaluación en tres o más momentos temporales diferentes) | En el caso de que la prueba sea significativa, se deben de hacer comparaciones múltiples ajustando el nivel de significación |
Unas palabras sobre las odds ratio y el Índice de Riesgo Relativo
Para poder entender el concepto de odds ratio hay que entender los siguientes conceptos asociados a ella:
- Probabilidad: La probabilidad es una medida que señala que tan posible es que ocurra un fenómeno o evento. Este valor oscila entre 0 y 1, siendo 0 que el evento no puede suceder y 1 que el evento ocurre seguro. Por ejemplo, si la probabilidad de mejorar es 0.60, la de no mejorar sería 0.40.
- Odds: es la probabilidad de que suceda un evento dividido por la probabilidad de que no suceda.
Las odds oscilan entre 0 e infinito y se pueden calcular para la ocurrencia del evento como para la no ocurrencia del evento. En el ejemplo, existirían dos odds: la odds de mejorar sería 0.60/0.40=1.5 y la de no mejorar sería 0.40/0.60=0.667. Se interpretan como ratios, es decir, la cantidad de veces que algo pueda suceder sobre que no pueda suceder. En este caso, es más probable que el paciente mejore.
Las odds ratio (OR) supone el cociente entre las dos odds y también oscilan entre 0 e infinito, pero ¿cómo se interpreta una OR de forma básica?
- Cuando la OR es 1 indica ausencia de asociación entre las variables.
- Los valores menores de 1 señalan una asociación negativa entre las variables y los valores mayores de 1 indican asociación positiva entre las variables.
- Cuanto más se aleje la OR de 1, más intensa es la relación.
En el caso del Índice de Riesgo Relativo, se define como el cociente de las probabilidades de tener la enfermedad o presentar el resultado de interés si está presente o ausente el factor predictivo, el factor de riesgo.
Para interpretar el riesgo relativo, pensemos en un RR de 2. Este resultado expresa que el riesgo en un grupo es el doble que en el otro grupo. Si es igual a 1, es igual para ambos grupos y si es menor que 1, el riesgo es mayor para el otro grupo.
La principal diferencia con la OR es que el Índice de Riesgo Relativo se usa fundamentalmente en la evaluación de trabajos prospectivos mientras que el OR se usa principalmente en el análisis de trabajos retrospectivos.
¿Se puede hacer algo más con las variables nominales?
¡Por supuesto que sí! El análisis de las variables nominales puede ir más allá de estudiar su comportamiento descriptivo y su relación bivariada. Algunos ejemplos de análisis que se pueden hacer:
- Modelos loglineales: si se quiere analizar la relación entre tres o más variables nominales.
- Algoritmos de machine learning de clasificación: si se quiere, por ejemplo, pronosticar la probabilidad de que un paciente se recupere (o no) en función de una serie de variables clínicas, estos algoritmos son de gran utilidad.
Análisis de textos y respuestas abiertas: los análisis vinculados al Procesamiento del Lenguaje Natural están al servicio del análisis de textos, por ejemplo, de respuestas abiertas dadas durante una entrevista a los pacientes para conocer su estado de salud.